严格性是怎样被介绍到数学分析里面的?这是一个复杂的问题,因为数学的实践已经有了相当大的变化,特别是在从微积分的创立到20世纪初期这一段时间里,虽然在一定意义下,对于什么是正确的合逻辑的论据,基本的判据并没有变,但是,需要我们做这种论证的环境,甚至在一定程度上,做这种论证的目的,却在随时间而改变。1700年代,与约翰·伯努利和丹尼尔·伯努利、欧拉和拉格朗日这些人相关的数学分析,其方法的缺少基础的清晰性,在以后的时期中,招来了批评也得到了弥补。到1910年左右,对于如何使得数学分析中的论证严格已经出现了一般的共识。
数学所包含的不仅有计算技巧,还有描述几何对象的重要特性的方法和世界现象的模型等等。所有做数学研究的数学家,都受到过如何得出严格的论证来论证自己的结论的训练。这些结论通常表述为定理,也就是关于一些事实的命题,同时也关心对这些命题作论证,即证明定理为真。
下面是一个简单的例子:每一个正整数,若能被6整除,也必能被2整除。沿着6的倍数的表往下看:{6,12,18,24……},就可以看到,其中每一个数都是偶数,这使得很容易就会相信这个命题。关于这个命题的一个可能的论证如下:因为6可以被2整除,所以,每一个可以被6整除的数,必定可以被2整除。
这样一个论证算不算一个彻底的证明,读者可以各有看法。因为看到这个论证以后,可以提出这样的问题即,这是否总是真的:如果 a,b,c是三个正整数,而且 c 可以被b整除,b可以被a整除,则c也一定可以被a整除吗?到底什么是整除性。 什么是整数?数学家处理这些问题的办法是:对概念作精确的定义,把这些定义的基础放在数量有点少的未定义的名词上。例如可以定义,所谓数n可以被数m整除,当且仅当存在一个整数q,使得qm=n。利用这个定义可以给出一个更精确的证明:若n可被6整除,则对某个q有n=6q,从而n=2(3q),这就证明了n可以被2整除。这样,可利用整除性的定义来证明,只要被6整除的定义成立,则可以被2整除的定义也成立。
从历史来看,数学家们会满足于不同水平的严格性。数学的结果和方法时常已经得到广泛的应用,而没有如刚才概述地那样完全的论证,特别是那些新的快速发展着的数学思想的总体是这样。在有些古代文化中,例如在埃及文化中,已经有了乘法和除法的方法,但是这些方法的论证则从未流传下来,而且特别可能的是这种形式论证并没有存在过。很可能是,这些方法被接受,只是因为它们管用,而不是因为它们有彻底的论证。
到了17世纪中期,欧洲从事研究的数学作者,都很熟悉由欧几里得的《几何原本》所提供的严格的数学论证的范本了。那是一种演绎的,或者说是综合的论证方法,是一种更加几何化的论证方法。虽然按照今天的标准来看,欧几里得的论据、假设和定义并不完全严格,但基本的思想是清楚的:从清楚的定义和所公认的基本思想出发来一步一步地导出定理(或称命题),而不引入任何外加的东西。这种几何论证的经典模型,广泛地用于对于数论、解析几何和力学的推理。
本文讨论的是分析中的严格性。分析一词的意义是一直在变化着的。它本来有古老的来源,而到1600年左右,这个词指的就是利用未知量(现在会写成x的东西)来进行计算或者求长度这一类的数学。换言之,它与代数有密切的关系,虽然这个概念被笛卡儿等人输入到几何学里去了。然而在18世纪的进程中,这个词变得与微积分有关了,而微积分成了分析技巧的应用的主要用武之地。当谈分析中的严格性时,主要就是讨论与微分学和积分学有关的数学的严格性。在17世纪,牛顿和莱布尼兹为微分学和积分学制定了对立的方法,他们就这样把相当数量的早前这两个方面的工作综合了、推广了,这两个方面就是关于曲线的切线和法线,还有曲线所包围的区域的面积。这些技巧非常成功,于是很快地就被推广到各个方向,最值得注意的是力学和微分方程。
这项研究的共同的关键特点是无穷量的使用,在某种意义下,这里涉及制定一个方法来把无穷多个无穷小的量合并,以得到有限的答案。例如,设把一个圆周作(数量很大的)等分,就是标记出许多等距离的点,然后把这些点连接起来,并与圆心连接,成为许多三角形。这些三角形的面积之和就逼近了圆的面积,而分点用得越多,逼近就越好。让我们想象有无穷多个这样内接的三角形,每一个的面积都"无限的小"。但是因为总体涉及把无穷多个无穷小加起来,还是有可能得到有限的正的总量。这里涉及的无穷的量是“真正的”无穷小,还是只不过是“潜在的”无穷小0?如果有什么东西是真正的无穷小,那它是不是就是零呢?亚里士多德学派的作者一直害怕真正的无穷小,这方面的抱怨在那时是很普遍的。
牛顿、莱布尼兹和他们的追随者们提出了一些数学论据来证明这些做法的合理性,然而引入技巧的推理是关于无穷小的对象、极限过程、无穷和等等,这就意味着微积分的创造者们在他们的推理中是在开辟新的基础,而由于所用的名词意义含混,由于在作出一个结论的同时,似乎也完全能够得到其他的结论,这些推论的可理解性时常“岌岌可危”。他们讨论的对象包括无穷小(即比直接经验过的量无穷地小的量)、消失着的量的比(即形如0/0的分数,或者趋近于这种分数)、无限多个正量的有限和。特别是泰勒级数表示,引起了许多这类问题。所谓泰勒级数就是:一个函数可以这样写成一个级数,使得如果把这个级数就看成是函数时,在给定的点x=a处它会给出相同的值、相同的变率(即一阶导数)、相同的任意阶高阶导数:
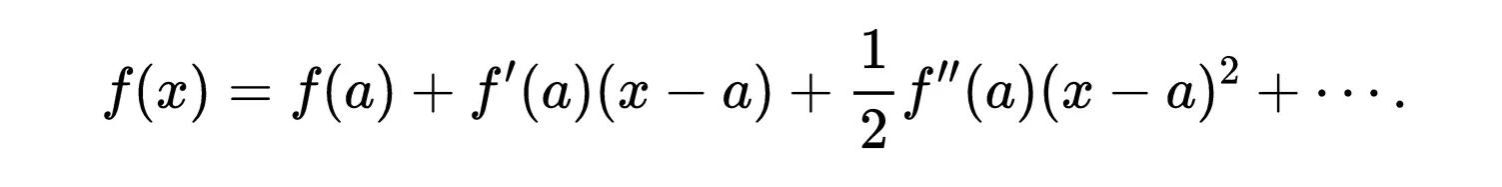
例如,
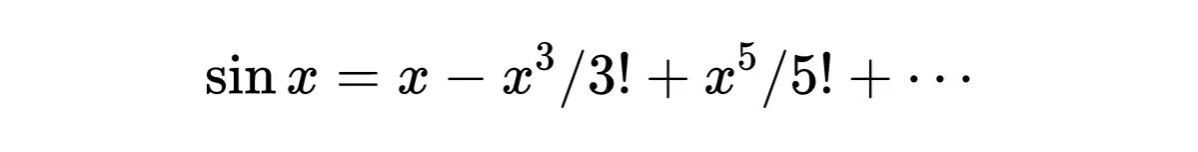
早期的论证中还有一个问题,就是对于所讨论的名词,不同的作者有不同的用法。从这种缺乏清晰性还产生了其他问题,因为它掩盖了许多问题。可能其中最重要的是一个论据在某个情况下失效,而很类似的论据在另一个情况下又完全能行。 到了一定的时候,在把分析加以推广时就会出大问题。分析在最终还是变得完全严格了,这些困难都解决了,但是这个过程很漫长,一直到20世纪初才完成。
下面是这种在最开始的时候就出现的困难的例子,这是莱布尼兹的一个结果。 设有两个变量u和v,而当另一个变量x在变化时,它们每一个都在变。记x的无穷小变化为dx,即x的微分。微分是一个无穷小量,看成一个几何量,例如看成长度。想象把它与其他的量按通常的方式或组合或比较(因为两个长度可以相加,可以有比等等)。当x变成x+dx时,令u和v分别变成u+du和v+dv。莱布尼兹做出了这样的结论:uv将要变成
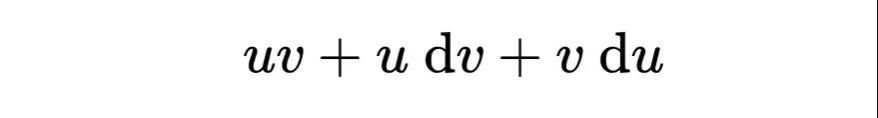
所以
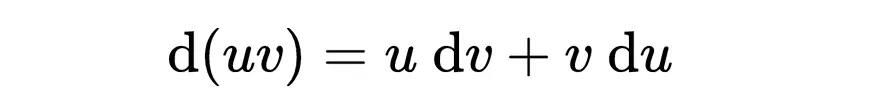
他的论据粗略地说是这样的:
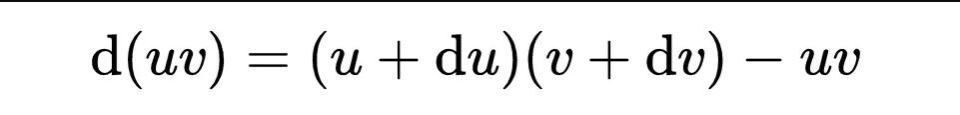
把右方按照正规的代数展开、化简,会给出

但是dudv这一项是二阶无穷小,比起一阶无穷小来说是消失的小(vanishingly small),用现代语言来说就是高阶无穷小,所以可以作为0来处理。这里的问题有一个侧面,就是在处理无穷小时出现了不相容的情况。再例如,如果想求出y=x^2的导数,这里的计算正相应于上面的计算(把(x+dx)^2展开等),得到dy/dx=2x+dx。 然后,把右边的dx当作0来处理,而左边的dx又似乎是看作无穷小的非零量,因为不然就不能用它来作除数。所以,它是零还是非零?如果不是,又怎么绕过这里的明显的不相容性?
在稍微更加技术性的层次上,微积分要求数学家一再地处理:当分子和分母都趋近0甚或真正为0时,形如dy/dx的比的"最终值"问题。在我们的陈述里,又一次使用了莱布尼兹的微分记号,虽然对于牛顿也发生了同样的问题,不过记号与概念上稍有区别。当牛顿讲到变量时,他总认为变量是依赖于时间的,例如他力求考虑在消逝(evanescent)的量——就是消失地小的增量下所趋近的值。一组无法消除的混淆正是来自这样一个思想,即变量是处在变化过程中,不论是随时间变化或者随其他变量而变化。这就是说,我们考虑的是趋近一个给定的值的变量所取的值,但对于究竟什么叫"趋近"又没有一个清晰的概念。
来源:众播教育