勾股定理是平面几何中一个基本定理，算得上直角三角形独特性的体现。很多人都知道勾股定理，边长分别为3、4、5可以组成一个直角三角形。这一定理的应用也比较广，但是很少有人知道关于勾股定理的起源。

根据一块泥板记载，“勾股定理”出现的时间往前推1000多年。

在此前的书籍当中，勾股定理可追溯到古希腊时期，就是那时的毕达哥拉斯定理。不过在那之前是否有过勾股定理的记载，就找不到什么实质性证据了。

最近考古学家的新发现，使得这一定理的历史可追溯到3700年前的古巴比伦时期。

澳大利亚考古学家发现了一块3700年前的楔型文字泥板。根据泥板内容来看，所描述的就是勾股定理。这个发现意义非常重大，要知道如果得以证实的话，人类对于勾股定理的研究可以往前推1000多年。

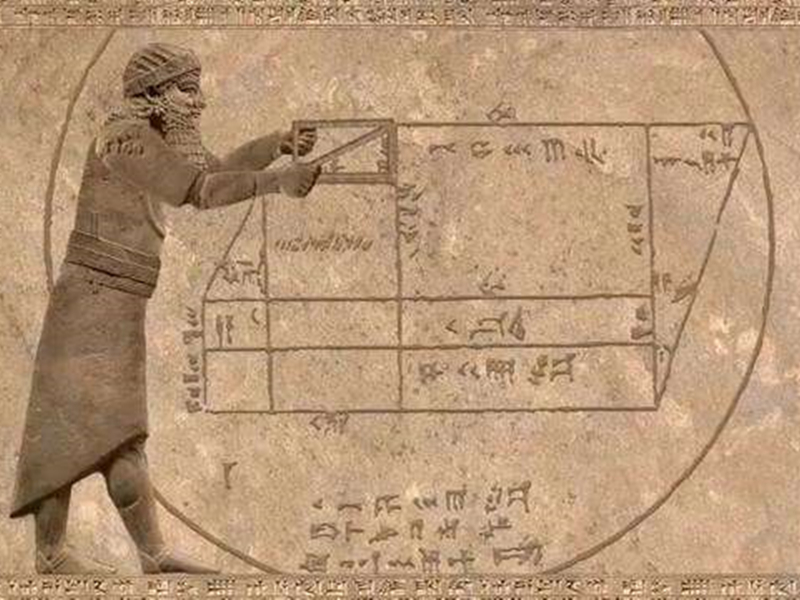
此前考古学家就发现了一块楔形文字泥板，上面标注了一些独特的三角表。

对比两次泥板的记载内容来看，古人对于数学的研究确实很早。那时处于奴隶制社会，文明还处于早期起源阶段，按理说发展生产才是古人主要考虑的事情。

为什么古人会对三角形有如此深的研究呢？其实这也是出于一些方面的需求。

“勾股定理”出现在3700年前的原因

在奴隶社会，虽然大家不需要进行精密的计算，但却有很大的划分土地的要求。肥沃的土地自然受到更多人的争抢，为了更公平地划分土地，人们就对基本的图形展开了研究。三角形作为一类最简单的平面图形，古人对它的研究也更多。

实际划分土地的时候，并不是所有土地都是正方形或者长方形，一些三角形的土地也需要计算面积。通过研究，勾股定理可以更好的划定土地边界。

由此可见，在很早的时候，人类先祖就已经有了运用几何解决现实问题的智慧了。

勾股定理算得上一个很容易发现的定理，只要测量了直角三角形的边长，就会发现直角边的平方和等于斜边的平方。

有了这一定理，只需要测量两条边，就能算出另一条边的长度。古希腊时期发展出了欧式几何，勾股定理算得上一条独立的定理。那时的几何学并未涉及到定量计算的问题，所以勾股定理的推广难以总结出规律。

随着代数的发展，人们找到了三角形更普遍的边长之间的公式，就是余弦定理。勾股定理是余弦定理在直角三角形上的特例。

古人对几何学的复杂理解可能没有后来人那么先进，但它确实表明，我们对数学的理解可能比目前的历史知识告诉我们的更加循序渐进。